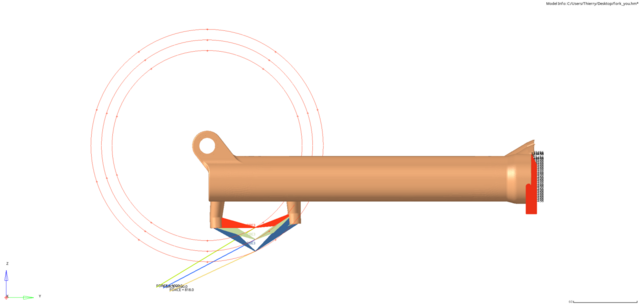
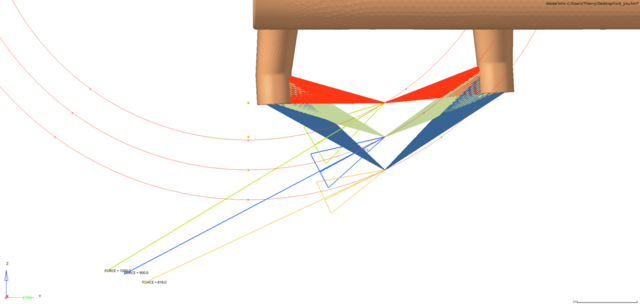
Also, die Diskussion hat mich interessiert und es ist wie immer ausgeartet. Ich nerde mal voran. Vorab: Ich war bisher ein Befürworter der Ansicht gewesen, dass die Scheibengröße egal ist, da das maximale Drehmoment durch die Haftreibung zwischen
Reifen und Untergrund begrenzt ist.
Wenn man einen simplen, fest eingespannten der Länge L Balken mit Querkraft F betrachtet, so ist die Biegespannung an der Einspannung nur vom Biegemoment M (F*L) und dem Widerstandsmoment W (I/a, mit I = b*h³/12 und in diesem Fall a = h/2) abhängig. Egal wie F und L also aufgeteilt sind, solange sie das Drehmoment M ergeben, ist die Biegespannung identisch.
Nun ist eine Bremsenaufnahme aber kein simpler Balken. Vereinfacht man eine Post-Mount-Aufnahme, so kann man die zwei Stumpen und die Bremse als beidseitig fest eingespannten Rahmen mit einem horizontalen Träger und biegesteifen Ecken (weil Schraubverbindung) ansehen, à la das Ding da:
Anhang anzeigen 1472948
Angenommen es wirken keine vertikalen Kräfte auf den Rahmen, ergibt sich folgendes:
Anhang anzeigen 1472949
Die Kraft P ist auf ihrer Wirklinie verschiebbar, man kann sie sich für die Visualisierung auch in die Mitte des horizontalen Balkens denken. Die Kraft wird hier mit P gekennzeichnet, die Höhe des Rahmens und der Kraft ist h, I_R und I_S sind die Flächenträgheitsmomente des Ständers (hihi, vertikal) und des Riegels (horizontal), l ist die Länge. Damit kann man die Kräfte und Momente im Rahmen und den Einspannungen wie folgt berechnen:
Anhang anzeigen 1472952
Anhang anzeigen 1472950
Sodele. Annahme: die Stumpen haben einen rechteckigen Querschnitt von 20mm*20mm ohne Bohrung, und der Einfachheit halber werden Bremse und Adapter mit dem gleichen Querschnitt modelliert. Für eine Aussage darüber, ob sich etwas signifikantes tut wenn sich die Scheibengröße ändert, ist das gut genug. Man nehme eine effektive Bremskraft von 300N am Rande des Vorderrades an, sowie 140, 160, 180, 200 und 220 Scheibengrößen. Als Abstand der Stumpen wurde 75mm gewählt, wie es der PM-Standard vorsieht. Die Höhe des Rahmens und des Kraftangriffspunktes ist gleich den Scheibenradien. Die Tangentialkraft an der Scheibe ergibt sich durch Fbrems*R/r.
| Bremskraft am Aufstandspunkt des VR | Fbrems | 300 | N | | | | |
| Radius Vorderrad | R | 300 | mm | | | | |
| Dimension Stumpen | a = b | 20 | mm | | | | |
| Flächenträgheitsmoment 2. Grades | I | 13333 | mm^4 | | | | |
| Widerstandsmoment | W | 1333.3 | mm^3 | | | | |
| | | | | | | |
| Scheibenradius r | 70 | 80 | 90 | 100 | 110 | mm | |
| Fscheibe | 1285 | 1125 | 1000 | 900 | 818 | N | |
| A | 508 | 518.9 | 526.8 | 533.3 | 538.7 | N | Normalkraft |
| B | -508 | -518.9 | -526.8 | -533.3 | -538.7 | N | Normalkraft |
| H1 | 642 | 562.5 | 500 | 450 | 409 | N | Scherkraft |
| H2 | -642 | -562.5 | -500 | -450 | -409 | N | Scherkraft |
| M3 | -19.1 | -19.5 | -19.76 | -20 | -20.2 | Nm | Biegemoment Ecke |
| M4 | 19.1 | 19.5 | 19.76 | 20 | 20.2 | Nm | |
| M1 | 25.9 | 25.5 | 25.2 | 25 | 24.8 | Nm | Biegemoment Einspannung |
| M2 | -25.9 | -25.5 | -25.2 | -25 | -24.8 | Nm | Biegemoment Einspannung |
| | | | | | | |
| Normalspannung | 1.27 | 1.29725 | 1.317 | 1.33325 | 1.34675 | Mpa | |
| Scherspannung | 1.605 | 1.40625 | 1.25 | 1.125 | 1.0225 | MPa | |
| Biegespannung | 19.42549 | 19.12548 | 18.90047 | 18.75047 | 18.60047 | Mpa | |
| Normal+Biegung max | 20.69549 | 20.42273 | 20.21747 | 20.08372 | 19.94722 | MPa | |
Man sieht, dass die Biegespannung am Stumpen mit steigendem Scheibendurchmesser abfällt. Die Unterschiede sind hier marginal, der Trend ist dennoch interessant.
Was passiert, wenn man die höhere Steifigkeit des Bremssattels berücksichtigt? Erhöht man das Flächenträgheitsmoment des horizontalen Balkens um das 5-, 10-, 100-fache, konvergiert das Biegemoment gegen +-22.5Nm.
Kann man jetzt irgendwas auf die reale Geometrie übertragen? Naja, die Spannungswerte sind sicher nicht übertragbar, da die Geometrie sich doch signifikant unterscheidet und die hier verwendeten Werte nur grobe Annäherungen sind. Die mit steigender Scheibengröße abfallenden Spannungswerte sind trotzdem eine Erkenntnis. Sicherlich keine neue, aber immerhin
. Da ich keinen Bock auf eine Serie von FEM-Analysen an realistischen Geometrien hatte, muss die Berechnung mit MDesign erst mal ausreichen.
Fazit: Sehr leichte Unterschiede gibts, nachts ist alle Theorie grau, Cider ist alle. Gut Nacht.
