Thema Technik – Anti-Rise, Anti-Squat Warum ist das beim Biken wichtig und wie bestimmt man es?

Anti-Rise, Anti-Squat: Was ist das eigentlich?

Anti-Squat und Anti-Rise sind keine Begriffe aus der Mountainbike-Branche, sondern wurden im Automobilbereich geprägt und beziehen sich auf das Nickverhalten des Fahrzeugs. Unter Nicken versteht man die Eigenschaft eines Fahrzeugs, beim Beschleunigen und Bremsen auf gerader Strecke nach vorne oder hinten zu kippen. Wer schon einmal mit einem jungen männlichen Führerscheinneuling in einem getunten 4er Golf an eine rote Ampel gefahren ist, die kurz darauf auf Grün springt, weiß, wovon die Rede ist:

Beim Bremsen zeigt die Motorhaube zunächst nach unten Richtung Asphalt – sobald die Ampel auf Grün springt und der 1,6-Liter-Motor laut brüllend versucht, seine letzten müden Pferdestärken in den Asphalt zu brennen, zeigt die Front schräg nach oben in den trüben Kleinstadthimmel.

Genau das Gleiche passiert beim Fahrrad oder jedem anderen Fahrzeug. Vor allem beim Anbremsen kann man den Effekt sehr gut selbst spüren oder bei anderen beobachten: Die Gabel federt deutlich ein, auch wenn man sich gegen die Bremskraft stemmt und den Schwerpunkt nicht nach vorne verlagert. Durch die Bremsbeschleunigung kommt es trotzdem zu einer Gewichtsverlagerung auf das Vorderrad.

Vielleicht ist euch aufgefallen, dass, wenn ihr mit sehr nassen Bremsen startet und das erste Mal in die Eisen langt, eure Körperhaltung plötzlich sehr hecklastig wird. Das liegt daran, dass ihr unbewusst damit rechnet, euch gegen die Bremskraft stemmen zu müssen. Da die Bremse aber erst mal nass ist und sehr schlecht funktioniert, bleibt diese aus und ihr schiebt euch unwillkürlich nach hinten.

Beim Beschleunigen ist der Effekt auf dem Mountainbike schwieriger zu erkennen – schließlich ist die Beschleunigung im Vergleich zum Auto eher gering und man bewegt sich zudem sehr hektisch. Aber man spürt, wie der Dämpfer bei jedem Tritt etwas einsackt und wieder ausfedert. Dieses Wippen ist ein bekanntes Phänomen bei Mountainbikern und kommt zum einen von der Unwucht, die der Mensch beim Pedalieren selbst erzeugt – im Vergleich zu einem Verbrennungsmotor wippt man eben ganz schön herum. Aber auch die Beschleunigung trägt ihren Teil dazu bei.

Diashow: Thema Technik – Anti-Rise & Anti-Squat: Was ist das und wie bestimmt man es?

Diashow starten »

Durch eine geschickte Auslegung des Fahrwerks am Mountainbike ist es allerdings möglich, diesem Verhalten zumindest teilweise entgegenzuwirken. In Bezug auf die Beschleunigung bezeichnet man diese Eigenschaft als Anti-Squat – die Gegenwirkung zum „Squat“ (= Hocken) des Fahrzeugs. Beim Bremsen hingegen spielt der Anti-Rise eine Rolle – Rise bezeichnet das Anheben des Fahrzeug-Hecks. Wichtig ist, zu verstehen, dass jedes vollgefederte Fahrrad über diese Eigenschaften verfügt – ganz unabhängig, ob bei der Entwicklung darauf geachtet wurde oder nicht. Antrieb und Bremse werden sich immer auf das Fahrwerk auswirken!

Wer sich schon etwas mit der Mountainbike-Entwicklung beschäftigt hat, dem dürften die netten 2D-Graphen mit den schräg durchs Bike gezeichneten Linien und lustigen Prozentangaben für Anti-Rise und Anti-Squat bereits untergekommen sein. Hier könnte man nun mit der Erklärung aufhören und sagen: Zieht einfach hier eure Linie und lest den Wert ab – fertig. Doch wirklich erklärt ist mit solchen Tautologien (das ist so, weil das so ist) nichts. Tatsächlich basieren diese Bilder auf einigen mechanischen und geometrischen Überlegungen – und starken Vereinfachungen.

Zum Verständnis muss man kein Ingenieur sein – Grundkenntnisse in Mathematik und Physik sind allerdings notwendig. Nachdem wir im letzten Thema Technik-Artikel noch etwas oberflächlich auf den Pedalrückschlag geblickt haben, geht es diesmal sehr stark ins Detail. In Zukunft werden wir uns dem Thema Fahrwerks-Kinematik allerdings wieder etwas weniger vertieft – aber nicht weniger interessant – widmen. Für alle, für die die Herleitung zu mathematisch ist, haben wir in den beiden unteren Abschnitten noch einige spannende Betrachtungen parat.

Anti-Rise-Berechnung

Wir beginnen mit der Anti-Rise-Berechnung – diese ähnelt stark der des Anti-Squat, ist aber etwas simpler. Zu Beginn muss man eine Grundannahme treffen: Wir definieren, dass der Anti-Rise als Prozentzahl angegeben wird und 100 % Anti-Rise bedeutet, dass die Bremse keine Bewegung im Fahrwerk erzeugen soll – zumindest theoretisch. Warum das praktisch kaum umzusetzen ist, klären wir später. Keine Bewegung im Fahrwerk bedeutet, dass kein Drehmoment im Hauptdrehpunkt herrscht. Dabei ist übrigens egal, ob es sich um einen virtuellen Drehpunkt handelt oder ein tatsächliches Hauptlager. Sprich, ob unser Rad beispielsweise einen Viergelenker oder Eingelenker-Hinterbau hat.

Ein Drehmoment ist bekanntermaßen eine Kraft mal einem Hebel. Im Umkehrschluss bedeutet dies, dass jede Kraft, die auf das System Mensch/Fahrrad einwirkt und nicht genau durch den Drehpunkt läuft, ein Drehmoment im Drehpunkt erzeugt. Dabei fungiert der senkrechte Abstand zwischen Kraftvektor und Drehpunkt als Hebel. Die klassisch getroffene Annahme zur Berechnung des Anti-Rise ist, dass zwei relevante Kräfte wirken und entsprechende Momente hervorrufen:

• F_Brems – Kraft zwischen Hinterrad und Untergrund, die für die Verzögerung des Bikes sorgt
• ∆F_Radlast – die Verschiebung der Rad-Aufstandskräfte zwischen Vorder- und Hinterrad

Der Einfachheit halber wurde ∆F_Radlast im unten stehenden Bild #3 nur am Hinterrad eingezeichnet – gilt jedoch natürlich auch am Vorderrad in umgekehrte Richtung. Es ergibt sich gemäß der Grundannahme nun die Formel:

Anti-Rise = 100 % * (|M_Brems|/ |M_Radlast|)

Die beiden Momente auf den jeweiligen Seiten des Bruchs wirken in entgegengesetzte Richtung – heben sie sich auf, erreichen wir 100 % Anti-Rise, womit die eingangs aufgestellte Definition erfüllt ist. Nun heißt es, die jeweiligen Werte in die Formel einsetzen und zusammenkürzen.

Das Bremsmoment ergibt sich aus der Bremskraft mal der Höhe des Drehpunkts über dem Boden. Ich hoffe, ihr habt noch ein paar Erinnerungen an die Geometrie in der Schule:

M_Brems = F_Brems * (Radius + Kettenstrebe * sin(𝛼_KS))

Der Teil in der Klammer ist einfach der Radius des Hinterrads, plus die Höhe der Kettenstrebe – das ergibt die Höhe des Drehpunkts über dem Boden, wo unsere Bremskraft wirkt. Die Angabe „Kettenstrebe“ im Bild #3 ist übrigens die Distanz zwischen Drehpunkt und Hinterrad, nicht, wie üblich, zwischen Tretlager und Hinterrad. Das Moment der Radlastverschiebung wieder ist die Differenz der Radaufstandskraft am Hinterrad mal dem Abstand zum Drehpunkt – der horizontalen Länge von „Kettenstrebe“:

-M_Radlast = ∆F_Radlast * (Kettenstrebe * cos(𝛼_KS))

Um den Anti-Rise berechnen zu können, müssten wir noch irgendwie die beiden Kräfte loswerden. Diese kürzen sich praktischerweise auch komplett raus. Müssen sie auch, denn der Anti-Rise ist nur abhängig von der Geometrie und nicht von der Bodenbeschaffenheit oder Reifenwahl, die wiederum die Bremskraft beeinflussen. In der Bild #3 ist eine weitere Kraft im Schwerpunkt erkennbar, die der Bremskraft entgegenwirkt. Dabei handelt es sich um die Trägheitskraft F_Schwerpunkt – also die Kraft, die uns beim harten Anbremsen nach vorne zieht. Das Kräftegleichgewicht in Fahrtrichtung (und auch etwas gesunder Menschenverstand) verraten uns, dass diese exakt der Bremskraft entspricht.

F_Brems = F_Schwerpunkt

Da wir lediglich den statischen Fall betrachten, unser Radfahrer sich also im mechanischen Gleichgewicht befindet und keine Beschleunigungen erfährt, können wir ein Momentengleichgewicht um den Radaufstandspunkt am Vorderrad aufstellen:

∆F_Radlast * Radstand = F_Schwerpunkt * Schwerpunkthöhe

Beziehungsweise mit unserer vorherigen Erkenntnis:

∆F_Radlast * Radstand = F_Brems * Schwerpunkthöhe

Dies lässt sich umstellen zu:

∆F_Radlast = F_Brems * (Schwerpunkthöhe / Radstand) = F_Brems * tan(𝛼_Schwerpunkt)

Hier taucht das erste Mal der Tangens (Gegenkathete durch Ankathete) der gelben Schwerpunktlinie in Bild #3 auf. Jetzt müssen wir einfach nur noch alles in unsere Ausgangsgleichung einsetzen – da dies in unserem für Texte und nicht Formeln ausgelegten Editor etwas lang und unübersichtlich wird, nun als Bild:

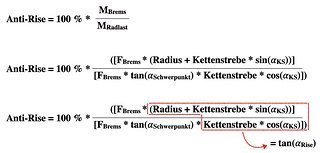
Der rot umrandete Teil der Gleichung ist nichts anderes als die vertikale (oben) und horizontale Lage (unten) des Drehpunkts im Verhältnis zum hinteren Radaufstandspunkt. In anderen Worten: der Tangens des Winkels der violetten Anti-Rise-Linie. Da die Bremskraft auf beiden Seiten des Bruchs steht, kürzt sich diese wie vorausgesagt weg. Übrig bleibt:

Anti-Rise = 100 % * (tan(𝛼_Rise) / tan(𝛼_Schwerpunkt))

Graphisch schön darstellen lässt sich der Anti-Rise, indem man den Tangens jeweils auf Höhe der Vorderradachse berechnet. In dem Fall kürzt sich der Radstand heraus und es bleibt übrig:

Anti-Rise = 100 % * (Anti-Rise-Höhe / Schwerpunkthöhe)

Der Anti-Rise ist also das prozentuale Verhältnis der Höhe, in der die Anti-Rise-Linie die vertikale Linie in der Vorderradachse durchsticht, zur Höhe des Schwerpunkts. Was im ersten Moment völlig beliebig erscheint, leitet sich durch einige geometrische Betrachtungen tatsächlich her. Erwähnenswert ist, dass der Anti-Rise sich beim Einfedern verändert – denn dabei ändert sich auch die Geometrie des Rads. Wird nur ein Anti-Rise-Wert angegeben und kein Graph, dann wird dieser oft im Sag gemessen. Außerdem hängt der angegebene Anti-Rise-Wert massiv von der angenommenen Höhe des Schwerpunkts ab. Für diese gibt es keinerlei Standards, sodass sich Werte zwischen Herstellern und Größen nur schwer vergleichen lassen.

Anti-Squat-Berechnung

Die Methodik zur Berechnung des Anti-Squats verläuft im Prinzip identisch zu der des Anti-Rise, ist allerdings aufgrund des zusätzlich auftretenden Kettenzugs nochmals komplexer. Ohne Übung in Geometrie und Mechanik wird es ziemlich schwierig, alle Schritte sinnvoll nachzuvollziehen. Eine relativ verständliche und gründliche Herleitung findet sich in der Doktorarbeit von Philipp Ingenlath von der RWTH Aachen. Diese lässt sich unter diesem Link öffentlich einsehen (zur Anti-Squat-Berechnung geht’s auf Seite 110). Auch wir haben uns daran orientiert.

Erneut legen wir wieder fest, dass der Anti-Squat als Prozentzahl angegeben wird und 100 % Anti-Squat bedeuten soll, dass der Antrieb (theoretisch) keine Wirkung auf das Fahrwerk haben soll. Keine Wirkung im Fahrwerk bedeutet auch hier, dass kein Drehmoment im Hauptdrehpunkt herrscht und egal ist, ob es sich dabei um einen virtuellen Drehpunkt handelt oder ein tatsächliches Hauptlager. Neben einer Radlast-Verschiebung und der Antriebs-Kraft zwischen Reifen und Boden gibt es diesmal noch den Zug der Kette, der sich ebenfalls als Kraft bemerkbar macht:

• F_Antrieb – Kraft zwischen Hinterrad und Untergrund, die für die Beschleunigung des Bikes sorgt
• F_Kette – Kraft entlang der Kette
• ∆F_Radlast – die Verschiebung der Rad-Aufstandskräfte zwischen Vorder- und Hinterrad

Gemäß unserer zu Beginn festgelegten Grundannahme muss dann also gelten:

Anti-Squat = 100 % * (|M_Antrieb + M_Kette|/|M_Radlast|)

Die beiden durch Antriebskraft und Kette hervorgerufenen Momente wirken in die eine, das durch die Radlastverschiebung hervorgerufene Moment in die andere Richtung. Gleichen sich beide Seiten des Bruchs, heben sich die Momente im Drehpunkt auf, der Bruch löst sich zu 1 auf – man erreicht 100 % Anti-Squat. Erneut müssen wir jetzt geometrische Werte einsetzen und zusammenkürzen.

Wir beginnen wieder mit dem Antriebsmoment. Dessen Hebel zum Drehpunkt ist der Radius des Hinterrads plus der vertikale Abstand zum Drehpunkt.

-M_Antrieb = F_Antrieb * (Radius + Kettenstrebe * sin(𝛼_KS))

Ähnlich verhält es sich mit dem durch den Kettenzug hervorgerufenen Moment. Die Kette liegt hinten auf einem bestimmten Ritzel auf und verläuft dann in einem gewissen Winkel zur Kettenstrebe. Man kann das Moment also ausdrücken als:

M_Kette = F_Kette * (Ritzel – Kettenstrebe * sin(𝛼_KS-𝛼_Kette))

Das Moment der Radlastverschiebung wird identisch berechnet wie beim Anti-Rise – dreht sicht allerdings diesmal in die andere Richtung.

M_Radlast = ∆F_Radlast * (Kettenstrebe * cos(𝛼_KS))

Es gilt nun, über Kräfte- und Momentengleichgewichte so lange einzusetzen und zu kürzen, bis nur noch geometrische Größe überbleiben. Die Antriebskraft und der Kettenzug lassen sich leicht in ein Verhältnis bringen, indem man das Momentengleichgewicht um die Hinterrad-Achse aufstellt:

F_Kette = F_Antrieb*(Radius/Ritzel)

Analog zum Anti-Rise gilt, dass sich die Antriebs-Kraft und die Trägheitskraft im Schwerpunkt entsprechen:

F_Antrieb = F_Schwerpunkt

Völlig identisch zur Anti-Rise-Berechnung erfolgt die Betrachtung der Radaufstandskraft-Verlagerung:

∆F_Radlast * Radstand = F_Schwerpunkt * Schwerpunkthöhe

∆F_Radlast * Radstand = F_Antrieb * Schwerpunkthöhe

∆F_Radlast = F_Antrieb * (Schwerpunkthöhe / Radstand) = F_Antrieb * tan(𝛼_Schwerpunkt)

Das kann man nun alles in die Grundgleichung einsetzen, was wir uns hier ersparen. Es kürzen sich alle Kräfte heraus – übrig bleiben nur geometrische Parameter. Diese kann man auch darstellen als:

Anti-Squat = 100 % * (tan(𝛼_Squat) / tan(𝛼_Schwerpunkt))

oder anders ausgedrückt:

Anti-Squat = 100 % * (Anti-Squat-Höhe / Schwerpunkthöhe)

Mit der Anti-Squat-Höhe ist erneut die Höhe gemeint, in der die Anti-Squat-Linie die senkrechte Gerade durch die Vorderrad-Nabe schneidet. Das Verhältnis davon zur Höhe des Schwerpunkts ergibt den Anti-Squat in Prozent. Genau wie der Anti-Rise variiert auch der Anti-Squat abhängig vom genutzten Dämpfer-Hub – ist nur ein Wert angegeben, bezieht sich dieser häufig auf den Sag. Manchmal liefern Hersteller allerdings auch Kurven, die den Verlauf des Anti-Squat durch den Federweg beschreiben.

Schwächen der statischen Berechnung

Dynamik: Eine statische Berechnung hat einen offensichtlichen Nachteil: Sie ist nicht dynamisch. Das bedeutet, dass etwa Änderungen der Fahrposition nicht berücksichtigt werden. Beim Anti-Squat macht es beispielsweise einen großen Unterschied, ob man im Sitzen oder im Stehen antritt, wie ruhig der Schwerpunkt dabei bleibt und welche Trittfrequenz man an den Tag legt. Beim Anbremsen, wenn der Anti-Rise eine Rolle spielt, variiert die Fahrposition ohnehin stark. Außerdem wird immer nur die Höhe des Schwerpunkts einbezogen, da die transversale Position der Berechnung zufolge keine Rollen spielt.

Das stimmt statisch auch: Egal, wie weit vorne oder hinten ich mich positioniere – das Maß, in dem mein Fahrrad nickt, ist immer dasselbe. Aber was ist, wenn ich in die Pedale trete und mich gleichzeitig nach vorne lehne? Oder bremse und nach hinten gehe? Beide Kennzahlen sind nützlich, um Designs bezüglich bestimmter Eigenschaften zu vergleichen. Sie verraten jedoch nur bedingt etwas über das tatsächliche Fahrverhalten und ersetzen ganz sicher keine aufwändige Entwicklung.

Vergleichbarkeit: Ein wichtiger Bezugspunkt ist die Höhe des Gesamtschwerpunkts. Diese ist aber keinesfalls normiert und unterscheidet sich je nach Fahrertyp oder auch Rahmengröße erheblich. Es erscheint natürlich wenig sinnvoll, bei einem XS-Rahmen dieselbe Schwerpunkthöhe wie bei der XXL-Version anzunehmen. Da die Hinterbau-Kinematik je nach Rahmengröße in der Regel nicht verändert wird, wird aber genau das gemacht. Es sind Erfahrungswerte oder Schätzungen der Entwickler gefragt, was bedeutet, dass die angegebenen Kennzahlen nur bedingt vergleichbar sind.

Es bedeutet allerdings auch, dass jeder Fahrer und jede Fahrerin einen anderen Anti-Rise und Anti-Squat erlebt – schließlich sind Größe, körperliche Proportionen und Fahrposition niemals identisch. Bei etwa gleich großen Fahrer*innen dürften sich die Unterschiede jedoch in Grenzen halten. Der Anti-Squat hängt natürlich auch von der Größe des Kettenblatts und dem gewählten Ritzel ab, weshalb verschiedene Übersetzungen in den jeweiligen Fahrsituationen berücksichtigt werden müssen.

Anti-Rise und Bremskraftverteilung: Die Berechnung des Anti-Rise bezieht sich lediglich auf die Hinterrad-Bremse. Ein Wert von 100 % bedeutet also, dass man theoretisch bei ausschließlicher Betätigung der Hinterradbremse keine Veränderung der Geometrie erfahren sollte. Aber wann bremst man schon so? Erfahrungsmäßig würde man schätzen, dass ein Großteil der Bremskraft auf das Vorderrad entfällt. Das kann sich aber je nach Terrain stark unterscheiden. An einer Teleskopgabel gibt es übrigens keinen ähnlichen Effekt – das Bremsmoment sorgt hier höchstens dafür, dass sich die Standrohre verbiegen.

Anders sieht es bei Parallelogramm-Gabeln, wie beispielsweise den mittlerweile eingestellten Modellen von Trust aus (Trust The Message-Test | Trust Shout-Test). Diese verfügen ebenfalls über eine Anti-Rise Charakteristik. Man könnte auch Teleskopgabeln mit einer Bremsmomentabstützung und somit Anti-Rise-Verhalten entwickeln – derartige Versuche gab es an Motorrädern bereits vor Jahrzehnten. Aufgrund der zusätzlichen Komplexität und der nicht wirklich nachgewiesenen Vorteile wäre das aber kein einfaches Unterfangen. Selbst am Hinterbau sind Bremsmomentabstützungen extrem unüblich geworden.

Wer sich vom Anti-Rise erhofft, dass er die Geometrie des Bikes stabil hält, der beachtet übrigens nicht, dass die Gabel ziemlich unabhängig vom Anti-Rise einsackt. Ein Rad mit über 100 % Anti-Rise wird zwar tendenziell am Dämper nicht ausfedern, an der Gabel allerdings einfedern. Insofern kippt das Rad durchaus nach vorne.

Grobe Vereinfachungen: Auch wenn wir am Ende einige lange Formeln umstellen mussten, um zu unserem Endergebnis zu kommen, muss man zugeben, dass die Ausgangsformeln ganz schön vereinfacht und simpel sind. In Wirklichkeit sind Fahrräder nicht 2-dimensional, von den fehlenden dynamischen Einflüssen hatten wir es schon und es können in Realität Effekte auftreten, die von der Theorie nicht berücksichtigt werden. Trotzdem konnte in Versuchen und Simulationen gezeigt werden, dass das tatsächliche Verhalten starke Parallelen zur statischen Berechnung aufweist und die Theorie (in Grenzen) gültig ist.

Und was bringt das jetzt?

Wir haben also gelernt, dass man durch einige geometrische Betrachtungen die Wirkung des Antriebs und der Bremse auf das Fahrwerk und die Balance des Bikes berechnen kann. Allerdings sind die theoretisch bestimmten Werte nicht 1:1 auf die Realität übertragbar – allein schon, weil der Mensch kein Massepunkt ist und sich ständig in Relation zum Rad bewegt. Das erklärt auch, warum die wenigsten Räder tatsächlich 100 % Anti-Squat und Anti-Rise haben. Beim Anti-Squat haben sich die Bike-Entwickler auf einen nutzbaren Bereich geeinigt, der meist etwas über 100 % liegt.

Grund ist, dass der Mensch sehr langsam und ungleichmäßig in die Pedale tritt – außerdem sorgen die sich bewegenden Beine sowie das Wackeln im Oberkörper für Unwuchten. Um dem dadurch erzeugten Wippen entgegenzuwirken, hebt man den Anti-Squat – sehr abhängig von den gewünschten Fahreigenschaften und der gewählten Übersetzung. Allerdings lässt sich der Anti-Squat bei den wenigsten Rädern unabhängig einstellen – man muss also einen Kompromiss finden, damit Werte wie der Pedalrückschlag, Anti-Rise oder auch der Bauraum und Design-Ideen berücksichtigt werden.

Bei der Interpretation des Anti-Rise hingegen gibt es große Unterschiede. Manche Hersteller versuchen, diesen möglichst gering zu halten und nutzen dafür spezielle Federungssysteme oder eine Bremsmomentabstützung. Davon verspricht man sich dann ein auch unter Bremswirkung sehr aktives Fahrwerk und die Vermeidung von Bremsstempeln. Dieses Phänomen wird oft als sich beim Bremsen verhärtender Hinterbau wahrgenommen. Was genau dahintersteckt, klären wir in einem eigenen Artikel.

Andere hingegen loben hohe Anti-Rise-Werte dafür, dass sie die Geometrie bewahren. So reichen Anti-Rise-Werte an modernen Mountainbikes von deutlich unter (z. B. Trek ABP) bis deutlich über 100 % (z. B. High-Pivot-Eingelenker). Auch hier gilt, dass der tatsächliche Anti-Rise-Wert nicht das vom Entwickler empfundene Optimum sein muss, sondern einfach von anderen Faktoren abhängt und nur ein Kompromiss-Wert ist.

Wie genau sich die genannten Kinematik-Werte auf das Fahrverhalten auswirken, welche Nebeneffekte es gibt und was es sonst noch zu beachten gilt, klären wir in einem weiteren Thema-Technik-Artikel. Als Nächstes werden wir uns die Eigenschaften verschiedener, verbreiteter Federungssystem ansehen.

Was sagst du zur graphischen und statischen Berechnung – sinnvolle Hilfe bei der Entwicklung oder Spielerei für Marketing-Zwecke?

Anmerkung: Bei dem Versuch, einige mathematische Abhandlungen nachvollziehbar und für jeden verständlich dazustellen, lasse ich einige mathematische Feinheiten unter den Tisch fallen. So finden sich hier beispielsweise keine Vektorpfeile und die Erklärungen werden einer wissenschaftlichen Veröffentlichung nicht würdig sein. Da viele von euch einen höheren Bildungsabschluss in einem technischen Fach haben, wird das sicherlich sehr schwer auszuhalten sein. Bitte haltet trotzdem die Füße still und konzentriert euch bei den Kommentaren auf das Wesentliche. Hinweise über irreführende Fehler und Diskussionen über das Für und Wider der gezeigten Methode sind mehr als willkommen.

Hier findest du alle weiteren Erklär-Artikel aus dem Thema Technik:

• Thema Technik – Federungssysteme am Mountainbike: Die 7 wichtigsten Hinterbau-Kinematiken erklärt
• Thema Technik – Anti-Rise, Anti-Squat: Warum ist das beim Biken wichtig und wie bestimmt man es?
• Thema Technik – Pedalrückschlag: Welche Rolle spielt der Pedalrückschlag am MTB?